Hang Liu
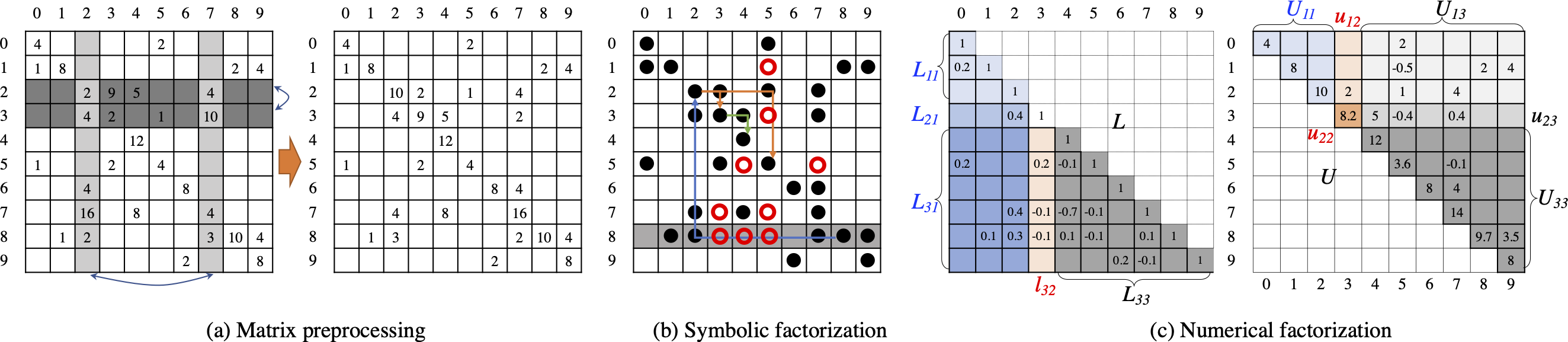
Project Description: Many scientific and engineering problems require solving large-scale linear systems, Ax = b. Solving this problem with direct methods often involves LU factorization, that is, decomposing the original matrix A into lower and upper triangular matrices L and U, respectively, where A = LU. Since LU decomposition of a sparse matrix typically introduces more nonzeros, also referred to as fill-in, than the original matrix A, symbolic factorization is designed to compute the structure of these nonzeros for both L and U. This information is subsequently used to predict the essential memory space for the subsequent numerical factorization. This project aims to develop a scalable symbolic factorization algorithm on GPUs which are absent in current practice.
